
THE STORY SO FAR
In
page 1
,
the real number system was introduced from the point of view of a
school student, gradually building from the natural numbers (1, 2, 3,...) to
include zero, fractions, negative numbers, and irrational numbers (both
surd and transcendental). This led to the concept of a real number line -
and ultimately, the Cartesian plane, in which graphs showing relationships
between real numbers could be plotted.
Also discussed were the extension of the real numbers to the complex
numbers, and the corresponding modification of the Cartesian plane to the
Argand plane. The fact that multiplication of complex numbers can be shown
to have a strong link to the idea of rotation was illustrated.
Another aspect of both real and complex numbers which was mentioned is the
fact that each of these sets of numbers forms a field. This basically
means that they obey certain rules or "laws" which essentially guarantee
that their arithmetic is "well-behaved", and doesn't hold any nasty
surprises.
The stage is now set for the entry of quaternions.
In the 1830's, Sir William Rowan
Hamilton
(1805-1865), the Astronomer Royal of Ireland, became interested in trying to
extend the notion of complex numbers to three dimensions. Expressing complex
numbers as "couplets", or ordered pairs [so that 5-7i might be expressed as
(5,-7)], he wanted to produce a system of "triplets" on which one could
perform arithmetic.
The idea was to have a second imaginary unit, j, which would square
to give -1 (just as i does), and which could be multiplied by i to produce
meaningful results. Adding and subtracting triplets presented no problem;
but he could not find a way to multiply them without introducing
inconsistencies.
On 16th October, 1843, he had a flash of inspiration. Triplet multiplication
would never work; but if two new imaginaries, j and k, were both
introduced - giving three imaginaries altogether - then you could produce a
system which would be internally consistent.
He was out walking with his wife when this dawned on him; and, on an
impulse, he carved into the stonework of Broome Bridge, Dublin, the
following cryptic inscription:
i2 =
j2 =
k2 = ijk = -1
These days, you'd probably be arrested for damage to property if you did
something like that; however, not only did Hamilton "get away with it", but
it is recognized as a famous historical event (in mathematical circles, at
least); and in 1958, the Royal Irish Academy erected a plaque commemorating
the incident! (You can see a photograph of the plaque by clicking on a link
within the web-page mentioned above; also, click
here
for a rather amusing page with some photos of the bridge - with its plaque -
and a bunch of mathematics/physics types having their picture taken next to
it.)
So what does it all mean?
This statement is Hamilton's way of defining what he called
"quaternions" by setting up some equations which govern how they interact.
The i, j, and k are all "imaginary quantities", just as i is in the context
of complex numbers. Each of them squares to give -1 ; having by now become
acquainted with complex numbers, it's not too hard to accept this idea as
being "reasonable". But what are we to make of the reference to ijk ?
Well, we can take "i2 = -1" as a
definition ("i is something which, when squared, gives -1").
Similarly, "j2 = -1" and
"k2 = -1" are also definitions.
Therefore, "ijk = -1" is another definition ("when you multiply i, j, and k,
the result is -1").
Think of these four definitions as "building blocks". We can play with them,
see how they interact with each other, and try to build something that looks
like a stable structure with them. If real numbers "pop up" at any point,
we'll allow ourselves to treat them as usual - in particular, allowing that
-1 × -1 = 1 ; and also assuming the Law of Multiplication by Unity or LMU
(from the
previous page ),
which states that multiplying by 1 doesn't change anything . (This may be
thought of as an "experimental" approach to mathematics.)
What happens when we do?
For a start, let's try multiplying i by ijk:
ijk = -1 , therefore i × ijk = i × -1 ,
therefore i2jk = i × -1 ,
therefore -1 × jk = i × -1
Taking a deep breath, let's see what happens if we allow ourselves to write
-1 × jk as -jk and i × -1 as -i , and then follow our instincts:
-jk = -i , therefore jk = i
Well, we're still here, aren't we? The universe didn't disappear in a puff
of smoke; so whatever we just did can't be too bad - and it just might come
in useful (whatever that means).
Let's do something similar, this time multiplying ijk by k; and this time
we'll be a bit less coy about dealing with minus signs if they crop up.
ijk = -1 , therefore ijk × k = -k ,
therefore ijk2 = -k ,
therefore
-ij = -k , therefore ij = k
So far, so good. By starting with ijk = -1, we've now managed to simplify
both ij and jk . But how will we simplify ik?
Still being cautious, we notice that there's a "j" stuck between the "i" and
the "k" in ijk = -1 . So let's try something different. Since we now have
expressions for both i and k in terms of other symbols, let's just multiply
them together and see what happens:
k × i = ij × jk = i × j2 × k
= i × -1 × k = -ik ,
therefore ki = -ik , or, equivalently, ik = -ki
That result doesn't contain a "j" , but it does tell us something very
important - that, since ki and ik are different, we were right to be
cautious about how we multiplied these things together. We've found an
example which shows that, in general, the Commutative Law of Multiplication
(CLM) doesn't hold for quaternions!
(Also, as we'll soon see, that last result we derived will turn out to be of
practical use in its own right as we proceed with our analysis.)
We just showed that jk = i . Let's multiply both sides of this equation by
k, so as to "kill off" the k. Noting that we can't expect the commutative
law to hold, we multiply both expressions by k on the right:
jk × k = i × k , therefore j × -1 = ik , or -j = ik .
Since we know that ik = -ki , we therefore have
-j = -ki , therefore ki = j .
Note that we could also have obtained this result via a different route by
starting with ij = k , and multiplying both sides of this equation
by i, so as to "kill off" the i. This time, we'd need to multiply both
expressions by i on the left:
i × ij = i × k , therefore -1 × j = ik , therefore -j = ik
as before, thus again concluding that ki = j .
So, at the end of all that, we have the following results:
ij = k ; jk = i ; ki = j ; and also ik = -ki , so that ik = -j
There's just a bit more to do. We'd be very surprised, at this point, if the
two statements ji = -k and kj = -i weren't true. However, we can't assume
anything; we have to check:
Combining jk = i and ki = j, we obtain jk × ki = i × j ,
therefore jk2i = k , therefore -ji = k,
or ji = -k
and similarly:
Combining ki = j and ij = k, we obtain ki × ij = j × k ,
therefore ki2j = i , therefore -kj = i,
or kj = -i
YAY! So now we have it all. A final summary:
ij = k ; jk = i ; ki = j ; ji = -k ; kj = -i ; and ik = -j
There is a pleasing symmetry about all this. We've assumed only Hamilton's
definition (originally a bit of graffiti on the Broome Bridge) and some
basic, very reasonable properties of real numbers: that the CLM applies when
multiplying reals by reals (just as in "usual" arithmetic); and that it also
applies when multiplying a real number by one of these "imaginary"
quaternions - both of which, it would seem, Hamilton assumed as "axioms", or
"self-evident truths".
The amazing thing is, however, that the CLM is false when multiplying
"imaginary" quaternions by each other! In these cases, the order of
multiplication does matter.
Before moving on: a few comments about what we've just done.
Firstly: the kind of very careful, even pedantic, reasoning in which we've
just engaged is typical of what mathematicians do. Manipulation of strings
of symbols in this fashion is de rigueur in the branch of mathematics
called "abstract algebra". (In the
previous page,
I did promise to mention something about "algebra" at some stage; now you
have it.)
Secondly: if you read most abstract algebra textbooks, you'll probably find
that the quaternions are not derived in this experimental way. You're far
more likely to find that our conclusions above are presented as
definitions. Why? Well, at the risk of stepping on a few toes, I
suggest that the authors like to appear to be completely in control, and not
allow of any suggestion of playful experimentation, of feeling their
way toward a result - because it looks less than "rigorous" to do so. The
algebraic reasoning will be presented, sure (and probably more tersely than
I've done here) - but only after strict assumptions have been stated.
I take issue with this! Mathematics has not been handed down to us on
stone tablets! It takes hard work and imagination to come up with a
significant mathematical result. Clearly, this was true in Hamilton's case.
(A more modern example is the
proof by Andrew Wiles
of Fermat's Last Theorem in the mid-1990's - it wasn't plain
sailing!) I firmly believe that there needs to be far more motivation
included in the teaching of mathematics; if this means recounting some of
its history (warts and all) so that students realize that top-notch
mathematicians are also human, and thus feel less intimidated, then so be
it!
[The 19th century mathematician Carl Friedrich Gauss is considered to be one
of the greatest mathematical minds ever; but in my extremely humble opinion,
he has a lot to answer for. Brilliant he may have been, but his style was
intimidating. (Have a look at
this web-page
to see what I mean. Also, visit
this page.) If my website can go at least
some of the way towards making mathematics more accessible to the
lay-person - and less intimidating to the poor student - I reckon I've done
something worthwhile.]
A similar situation exists in science. Ideas often take years or decades -
or longer - to come to full fruition, and usually require the input of many
scientists, all contributing, modifying and adding to work that has been
done previously. For a classic example, see my
electromagnetism
page. (Again, I'd like to see more intellectual honesty about this - and
related matters - in many physics textbooks.)
Some comments about the subject matter itself are also in order, before
proceeding.
What we've done so far is to investigate the way multiplication works
for quaternions - and, so far, only for the eight simplest quaternions: i,
j, k, -i, -j, -k, 1, and -1.
That's certainly the most novel thing about quaternions; however, quite
clearly, Hamilton was interested in adding and subtracting them as well - so
that things like i+2j, 7-2i+j-5k, -j+4k etc. are included. Then
multiplication among these would work as illustrated by the following
example:
(i+2j) × (-j+4k) = -ij+4ik-2j2+8jk =
-k-4j+2+8i , or 2+8i-4j-k
Thus, just as the set of complex numbers contains not just the four simplest
elements (i, -i, 1, and -1) but also every possible expression of the form
x + iy, where x and y are any real numbers - so also, the full set of
quaternions consists of all possible expressions of the form
w + xi + yj + zk
where w, x, y, and z are real numbers; and the expressions can be added and
subtracted, as well as multiplied and "divided".
It's worth mentioning, however, that the small set containing only i, j, k,
-i, -j, -k, 1, and -1 is also important in its own right. Together
with multiplication as just described, this set forms what is known as the
quaternion group,
which is of particular interest to mathematicians because it has certain
special properties.
Since a quaternion can be composed of up to four components added together,
multiplying them can be a bit of a handful. Whereas two complex numbers
(which are each composed of a maximum of only two components) multiply
together to give a maximum of four summands, with quaternions up to 16
summands are possible! So there's quite a bit of "donkey-work" involved if
you're going to multiply them "by hand".
The quaternions, with addition and multiplication, obey all the field laws
except one: the CLM. (When working with them, it's essential to bear this in
mind to avoid silly mistakes.) In particular, the CLA does hold
(thank goodness!
An "almost-field" of this type is sometimes referred to as a "division ring"
or a "skew field". Unfortunately, both these terms include fields as well;
perhaps "strictly skew field" may be a useful term. (This is one of those
silly accidents of history - a bit like how we have to "agree" that
electric current flows from positive to negative, even though we now know
that the electrons which usually make up electric currents actually flow in
precisely the opposite direction. In both cases, because somebody didn't
clarify a situation in the early stages of development, misunderstandings
and confusion have become entrenched.)
Another thing that's worth a quick mention is the Distributive Law, which
deals with how addition and multiplication "interact" with each other. With
fields (eg. the real or complex numbers), it's enough to give the "left"
DL: a(b+c) = ab + ac , because with the CLM working, we can then
deduce the "right" version of the law: (b+c)a = ba + ca .
However, in a strictly skew field (such as the quaternions), it's necessary
to spell out the left and right distributive laws, both of which are
required but can't be derived from each other in the absence of the
CLM. (Just thought you'd be fascinated...
The word "division" in the paragraph before last brings up an important
matter: how do you divide one quaternion by another? (So far, as you
may have noticed, I've skirted around this issue.)
An approach somewhat similar to that for dividing complex numbers can be
used. Fortunately, every quaternion has a quaternion conjugate. When
a quaternion and its conjugate are multiplied together, the result is a pure
real number (with no i's, j's, or k's). Also fortunately, the order in
which they are multiplied doesn't matter - you get the same result either
way.
The conjugate of w+ix+jy+kz is w-ix-jy-kz . Multiplying them together (in
either direction) yields
w2+x2+y2+z2. This is strongly analogous to the
way complex conjugates behave, and easy to remember. (As in complex numbers,
the square root of this number is called the modulus of the
quaternion, and may be thought of as its "distance" from the origin,
applying Pythagoras's Theorem in a four dimensional setting.)
This means that the multiplicative inverse (or reciprocal) of
w+ix+jy+zk is
(w-ix-yj-kz)/(w2+x2+y2+z2),
because if you multiply this by w+ix+yj+zk, you will get 1. (This is another
of those cases in which the order of multiplication makes no difference.)
So, to "divide" one quaternion "by" another, we can multiply both by the
conjugate of the divisor and then (if necessary) simplify the result.
Again, we have to bear in mind that the CLM cannot be assumed. Thus, if A
and B are two quaternions, and if the multiplicative inverse of B is
represented by B', in general A×B' will not give the same result as B'×A
(which means that expressions like A/B are ambiguous, and should be
avoided). So, again, we have to be careful to get the order right when doing
the multiplication!
For example:
Let A = 2 + k , and B = 2 - i + j - 2k . (We'll work out both A×B' and
B'×A.)
First: B' = (2 + i - j + 2k) /
[22 +
(-1)2 +
12 +
(-2)2] = (2 + i - j + 2k) / 10 .
Then:
A×B' = (2 + k) × (2 + i - j + 2k) / 10
and:
B'×A = (2 + i - j + 2k) / 10 × (2 + k)
- and, as you can see, they're not the same.
Note: if the square root of
(w2 +
x2 +
y2 +
z2) = 1 , then w + ix + yj + zk is
called a unit quaternion, as its "length" (or norm, denoted by
||w + xi + yj + kz|| ) = 1 .
As you've probably realized by now, performing arithmetic on quaternions "by
hand" is a messy, complicated business - and you really have to concentrate
to avoid making errors. It's not exactly difficult; it's just tedious. This
sort of thing is done far better by computers than by people.
Of course, in the 19th century, when all this stuff first appeared, there
weren't any computers. So it's not surprising that quaternions were viewed
as something of a mixed blessing.
On the one hand, they were a novel, interesting phenomenon - especially back
then, when a number system which violated the CLM was unheard-of. On the
other hand, they're a pain to deal with, in practical terms!
Of course, this all begs the question: why would anybody want to be bothered
with quaternions at all, other than for their novelty value?
After all, it's not easy to visualize what's going on with them. They're a
four-dimensional system, with one "real" and three "imaginary" dimensions;
and very few people claim to be able to get a mental picture of what happens
in any more than three dimensions.
Two dimensions aren't a problem. The Cartesian plane, with its two "real"
dimensions, and the Argand plane, with one "real" dimension and one
"imaginary" dimension, are easy: you can draw detailed diagrams on a sheet
of paper, etc. - but four dimensions present quite a challenge.
So is there any practical use for them? Is there any way we can apply
quaternions to normal three-dimensional space?
Indeed there is. Computers are now everywhere, and don't share the problem
that humans have when dealing with long-winded messy calculations; and one
of the really neat things about quaternions is that they can be applied to
computer animation, as I mentioned in the introduction to
page 1
of this article.
Following is a bit more background about quaternions, and some links from
which I hope you will gain at least some idea of how they can be applied to
rotation.
Within the set of real numbers, each positive number has two square
roots: one positive and one negative. The square roots of 1 are ±1, i.e.
"plus or minus 1".
Zero has one square root (itself); and negative numbers don't have any.
Within the set of complex numbers, every non-zero number has two
square roots. (Zero still has one, as before: itself.)
What about the quaternions?
In particular, we know that i2,
j2, and
k2 are all equal to -1. In a similar
way to -i in the complex case, it's easy to show that the squares of -i, -j,
and -k are also equal to -1 in the quaternion case.
Is that it? Are there any more quaternion square roots of -1?
Let's consider what happens if we square xi + yj + zk (with at least one of
x, y, or z not equal to zero):
(xi + yj + zk)2 =
(xi + yj + zk) × (xi + yj + zk)
How about that? It's a negative real number!
If we divide (xi + yj + zk) by the square root of
(x2 +
y2 +
z2) , we obtain a quaternion which will
square to give -1, whatever the values of x, y, and z may be. So we have a
system in which -1 has infinitely many square roots!
What's more, these quaternions are purely imaginary, with no real
component. Thus we have something which looks three-dimensional - something
we can visualize. In fact, these square roots of -1 form a spherical shell
of radius 1 in a three-dimensional space in which we can show numbers of the
type "qi" along an x-axis, numbers of the type "rj" along a y-axis, and
numbers of the type "sk" along a z-axis, where q, r, and s are all real
numbers and
q2 +
r2 +
s2 = 1.
Of course, if q, r, and s have other (real) values, we get a
differently-sized spherical shell, the radius of which will be the square
root of
q2 +
r2 +
s2, because of Pythagoras's Theorem in
three dimensions. Thus we can choose any position in space a fixed distance
M (for modulus) from the origin.
(qi + rj + sk)2 =
-(q2
+ r2
+ s2)
The day after Hamilton discovered quaternions, he wrote a
letter
to his friend John T. Graves, in which he introduced the subject and also
discussed square roots. (Click
here
to see my own page dealing with this matter further.)
Now, having given some preliminaries, I'll admit to not having a full
understanding of how the rotation process works; so, rather than jump in
feet first and make a monkey of myself, I'll refer you to some other
web-pages where you can follow this up if you'd like to:
This link
gives a very brief introduction to how quaternions can be used to show
rotation.
Or, visit
this web-page
and scroll down to the bottom to find a link to a 10-page .pdf file which
gives a more detailed introduction to this quite deep subject, but does so
in as gentle a "beginner-friendly" fashion as you'll probably find anywhere.
As always, I recommend right-clicking to download this file to hard disc and
then scanning it for viruses before opening it. It's probably OK; but with
the possibility of "nasties" affecting internet traffic, it's better to be
safe than sorry.
In these links, it is pointed out that the real part of a quaternion can be
considered to be a scalar quantity, and that the three imaginary
parts taken together can be viewed as a vector quantity. These terms
will become important in the discussion of the final topic in this page,
coming up next.
Using quaternions is not the only way to perform rotation. There are other
methods - and different methods have their champions! In fact, there is some
rather heated debate going on about the matter. To gain some idea of its
intensity, and learn something about the issues involved, have a look at
this web-page.
It must be admitted that this discussion of the rotational aspect of
quaternions has become somewhat technical. Don't worry if you didn't follow
it completely; unless you're thinking of going into computer graphics,
you'll probably never need to! I just included it to give an idea of the
flavour of the subject.
UPDATE, Friday, 21st June 2019 (winter solstice day, down here in the southern hemisphere!)
It's been a while since I've revisited this page to see which (if any) of the
external links still work; it seems that at least some of them don't,
unfortunately. However, someone has sent me a link to a page which does
work - so far, at least! - and which contains some good general information
about quaternions (thanks, Jim!). Well worth a look; here's the link:
https://www.mauriciopoppe.com/notes/mathematics/numeral-systems/quaternions/
I'd like to conclude this page with another aspect of quaternions. I'll
admit that I don't fully understand everything about this either; but I
believe that it is of such fundamental importance that some reference to it
must be made. Indeed, I'll admit freely that it's the main reason I included
these pages about quaternions at all.
Please note: in order to cut a long story as short as possible, I'll
just give the "bare bones", and include several links to other web-pages.
Please click on them and read their content to fill in the details.
As mentioned in that last link given above, quaternions caught many people's
imagination in the mid-19th century. Hamilton believed that they would be
of major importance in the development of mechanics; for a time, the idea
was popular. Perhaps the phenomenon is similar to the way chaos theory and
fractals "caught on" in the late 20th century (see my
Mathematically-based computer graphics
page for more about this).
However, as hinted earlier, in the late 1800's the popluarity of quaternions
began to wane.
When James Clerk
Maxwell
(1831-1879) published his electromagnetism equations in 1873, he made a
point of stating them in quaternion form.
In
this link
(about Hamilton - the same link given near the top of this page), toward
the bottom, you can read how physicist William Thomson (Lord Kelvin) and
mathematician Arthur Cayley had strong reservations about quaternions.
This link
takes up the story of how, after Maxwell's death, J. Willard Gibbs and
Oliver Heaviside did some drastic surgery on Maxwell's equations,
effectively removing any quaternion content from them.
This link
gives a brief introduction to the work of Tom Bearden, who has pioneered
the suggestion that the removal by Gibbs and Heaviside of the scalar
component of the quaternion version of Maxwell's equations, leaving only the
three-dimensional vector component, has caused a great deal of damage,
slowing scientific progress down dramatically over the last century.
This link
is part of the same website as the page just mentioned, and is a link
within that page. It gives more detail regarding the importance of restoring
quaternions to their former place in electromagnetic theory.
This link
is part of Tom Bearden's own website, and perhaps as good as any place
within it to start. (His pages tend to be long and technical; this seems to
be one of the most accessible to the novice in these matters.)
This article
by Tom Bearden gives more background on these matters, including comments
about Oliver Heaviside's difficulties with quaternions. A bit on the heavy
side (pun intended!
Finally, a link to my
Zero-point energy
page, in which I pursue this further, and include links to pages dealing
with Tom Bearden's Motionless Electromagnetic Generator (MEG).
With our world in deep trouble, this is an issue that needs to be known
about and investigated fearlessly by intelligent, caring people - and, yes,
I do count myself among them! If you do too, I encourage you to get
involved. The matter is urgent.
Return to
Quaternions - page 1
Proceed to
Quaternions - page 3
My home page
Preliminaries (Copyright, Safety)
Quaternions: an old (and new) look at four dimensions - page 2







 ).
).
 )
)

= (4 + 2i - 2j + 4k + 2k + j + i - 2) / 10
= (2 + 3i - j + 6k) / 10
= 0.2 + 0.3i - 0.1j + 0.6k
= (4 + 2k + 2i - j - 2j - i + 4k - 2) / 10
= (2 + i - 3j + 6k) / 10
= 0.2 + 0.1i - 0.3j + 0.6k


Note that ±1 and ±i are all on a circle of radius 1, centred on the origin.
The two square roots of 1 are still ±1. This time, -1 has two square roots
also: ±i.
= -x2 + xyk - xzj -xyk
-y2 + yzi +xzj -yzi
-z2
= -(x2 +
y2 +
z2)
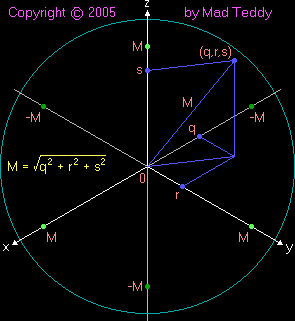 Note: most quaternions have only two square roots. (As usual,
zero has just one: itself). It's only negative real numbers that have
infinitely many (quaternion) square roots.
Note: most quaternions have only two square roots. (As usual,
zero has just one: itself). It's only negative real numbers that have
infinitely many (quaternion) square roots.


 ), as is most of Tom's writing, but
quite fascinating if you persevere with it.
), as is most of Tom's writing, but
quite fascinating if you persevere with it.


 Return to Mathematical stuff menu
Return to Mathematical stuff menu

